

These angles are called reference angles since we will reference their values to determine other values. The following is a list of the sine, cosine, and tangent functions values of special angles in the first quadrant.Īcute angles in the first quadrant can be used to determine the values of trigonometric functions of angles in other quadrants. While we can find the value of any of the trigonometric functions for any value of θ, there are some angles that are more frequently used in trigonometry and worth memorizing. The values of trigonometric functions can be found through the coordinate values of the intersections on a unit circle. Trigonometric function values for the special angles The values of the trigonometric functions can also be represented by the lengths of the line segments in a coordinate plane with a unit circle as show in the diagram below. Thus, on the unit circle, cosine and sine can be defined as:Ĭosecant, secant, and cotangent are the reciprocals of sine, cosine, and tangent respectively, and are defined as: The point at which the terminal side of the angle intersects the unit circle has an x-value of cos(θ) and y-value of sin(θ). The terminal side of the angle is the hypotenuse of the right triangle and is the radius of the unit circle. θ is the angle formed between the initial side of an angle along the x-axis and the terminal side of the angle formed by rotating the ray either clockwise or counterclockwise. In such a triangle, the hypotenuse is the radius of the unit circle, or 1. Given a point (x, y) on the unit circle, we can form a right triangle, as shown in the figure. Using the unit circle definitions allows us to extend the domain of trigonometric functions to all real numbers. The right triangle definition of trigonometric functions allows for angles between 0° and 90° (0 and in radians). A unit circle is a circle of radius 1 centered at the origin. Trigonometric functions can also be defined as coordinate values on a unit circle. These functions are often written in their abbreviated forms. The following are the definitions of the trigonometric functions. Consider an angle θ as one angle in a right triangle.

The output of a trigonometric function is a ratio of the lengths of two sides of a right triangle.
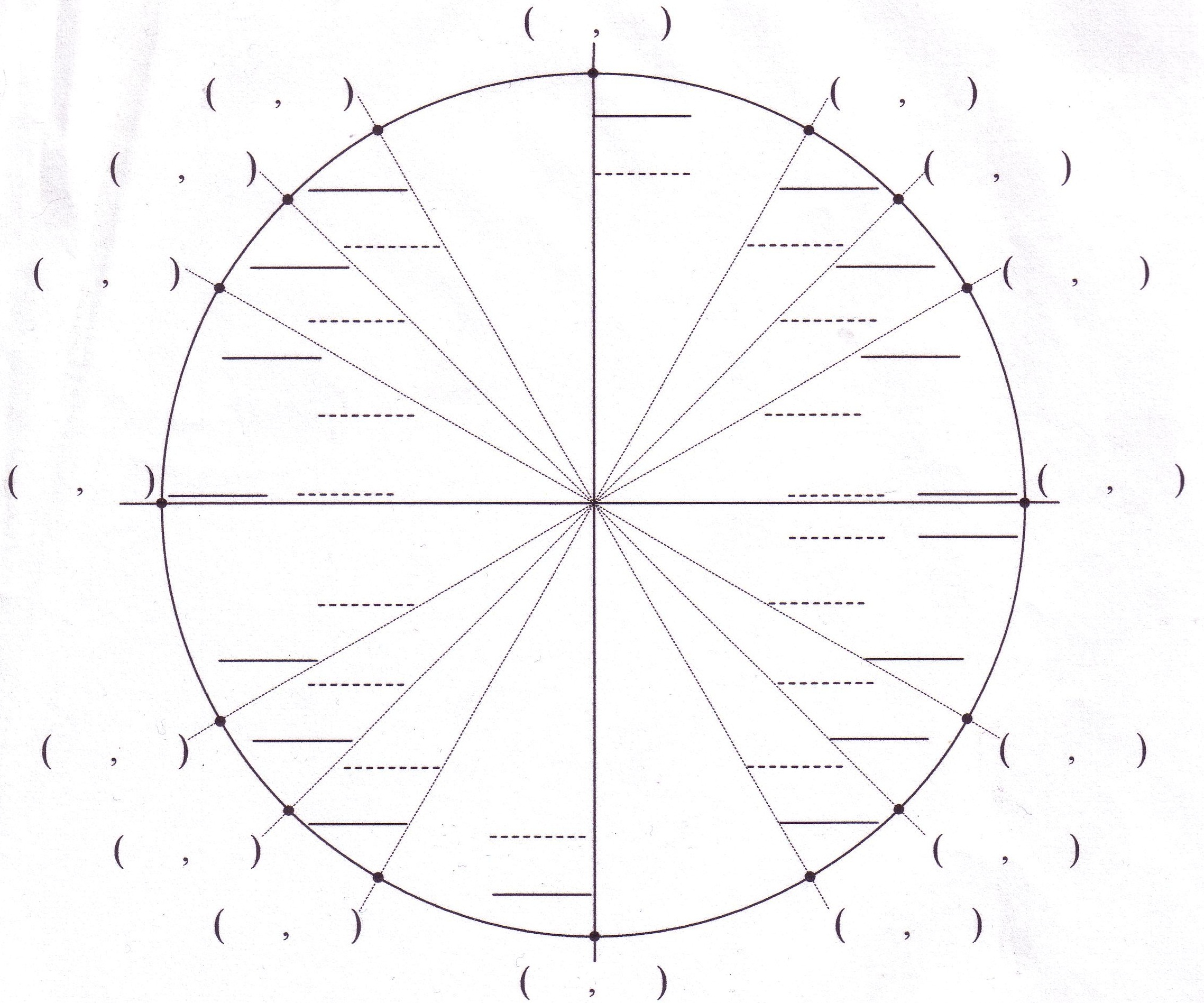
The right-angled triangle definition of trigonometric functions is most often how they are introduced, followed by their definitions in terms of the unit circle. There are two main ways in which trigonometric functions are typically discussed: in terms of right triangles and in terms of the unit circle. Trigonometric functions are also called circular functions. Their reciprocals, though used, are less common in modern mathematics. Sine, cosine, and tangent are the most widely used trigonometric functions. There are six trigonometric functions: sine, cosine, tangent and their reciprocals cosecant, secant, and cotangent, respectively. Trigonometric functions are functions related to an angle. Simplify these fractions to get 0, π/2, π and 3π/2.Home / trigonometry / trigonometric functions Trigonometric functions The numerators start at 0, beginning at the coordinate (1,0), and count up counterclockwise by 1π. A degree measures angles by distance traveled. (A radian is the angle made when taking the radius and wrapping it round a circle. The four associated angles (in radians, not degrees) all have a denominator of 2. If we instead went up, left, or down, we would touch the perimeter at (0, 1), (-1, 0), or (0, -1) respectively. In a unit circle, a straight line traveling right from the center of the circle will reach the circle's edge at the coordinate (1, 0). The y-coordinate is the sine of the angle. The x-coordinate is the cosine of the angle formed by the point, the origin and the x-axis. The y-coordinate represents the distance traveled up or down. The x-coordinate represents the distance traveled left or right from the center. We can use (x, y) coordinates to describe any point along the outer edge of the circle.


 0 kommentar(er)
0 kommentar(er)
